Home / Biology / The Living World
Topics
1
Laws of Chemical Combination
2
Atomic and Molecular Masses
3
Mole Concept and Molar Masses
5
Stoichiometry and Stoichiometric Calculations
6
Concentration of Solutions
8
Empirical and Molecular Formulas
11
Law of Definite Proportions
12
Balancing Chemical Equations
15
Classification of Matter
Laws of Chemical Combination
Laws of Chemical Combination
The laws of chemical combination are fundamental principles that describe how elements combine to form compounds. These laws are essential for understanding chemical reactions and stoichiometry. Here are the five primary laws:
- Law of Conservation of Mass
- Law of Definite Proportions
- Law of Multiple Proportions
- Gay-Lussac’s Law of Gaseous Volumes
- Avogadro’s Law
1. Law of Conservation of Mass
Statement: Proposed by Antoine Lavoisier in 1789, this law states that mass is neither created nor destroyed in a chemical reaction. The total mass of reactants equals the total mass of products.
Mathematical Representation: [ \text{Mass of reactants} = \text{Mass of products} ]
Example: When 5.2 g of calcium carbonate (CaCO₃) is heated, it decomposes to form 3.2 g of calcium oxide (CaO) and 1.99 g of carbon dioxide (CO₂). The total mass of products (3.2 g + 1.99 g = 5.19 g) is nearly equal to the mass of the reactant (5.2 g), considering experimental errors1.
Application in Stoichiometry: This law is crucial for balancing chemical equations. For example, in the reaction: [ \text{C}_3\text{H}_8 + 5\text{O}_2 \rightarrow 3\text{CO}_2 + 4\text{H}_2\text{O} ] The total mass of reactants (propane and oxygen) equals the total mass of products (carbon dioxide and water).
2. Law of Definite Proportions
Statement: Proposed by Joseph Proust in 1799, this law states that a given chemical compound always contains its component elements in a fixed ratio by mass, regardless of its source or method of preparation.
Mathematical Representation: [ \text{Mass ratio} = \frac{\text{Mass of element A}}{\text{Mass of element B}} ]
Example: Water (H₂O) always contains hydrogen and oxygen in a mass ratio of 1:8. This means that 9 g of water will always contain 1 g of hydrogen and 8 g of oxygen1.
Application in Chemical Analysis: This law is used to determine the purity of compounds. For instance, if a sample of water does not have a 1:8 mass ratio of hydrogen to oxygen, it indicates the presence of impurities.
3. Law of Multiple Proportions
Statement: Proposed by John Dalton in 1803, this law states that when two elements combine to form more than one compound, the masses of one element that combine with a fixed mass of the other are in the ratio of small whole numbers.
Mathematical Representation: [ \frac{\text{Mass of element A in compound 1}}{\text{Mass of element A in compound 2}} = \text{Simple whole number ratio} ]
Example: Carbon forms two oxides with oxygen: carbon monoxide (CO) and carbon dioxide (CO₂). In CO, 12 g of carbon combines with 16 g of oxygen (ratio 12:16 or 3:4). In CO₂, 12 g of carbon combines with 32 g of oxygen (ratio 12:32 or 3:8). The ratio of oxygen masses (16:32) is a simple whole number ratio of 1:21.
Application in Molecular Formulas: This law helps in determining the empirical formulas of compounds. For example, the empirical formula of a compound can be derived by comparing the mass ratios of its elements.
4. Gay-Lussac’s Law of Gaseous Volumes
Statement: Proposed by Joseph Louis Gay-Lussac in 1808, this law states that when gases react together at constant temperature and pressure, the volumes of the reacting gases and the volumes of the products (if gaseous) are in simple whole number ratios.
Mathematical Representation: [ \frac{\text{Volume of gas A}}{\text{Volume of gas B}} = \text{Simple whole number ratio} ]
Example: When hydrogen gas reacts with oxygen gas to form water vapor, 2 volumes of hydrogen react with 1 volume of oxygen to produce 2 volumes of water vapor (2H₂ + O₂ → 2H₂O). The volume ratio of hydrogen to oxygen to water vapor is 2:1:21.
Application in Gas Reactions: This law is used to predict the volumes of gases involved in reactions. For example, in the synthesis of ammonia (NH₃) from nitrogen and hydrogen gases, the volume ratio is 1:3:2 (N₂ + 3H₂ → 2NH₃).
5. Avogadro’s Law
Statement: Proposed by Amedeo Avogadro in 1811, this law states that equal volumes of all gases, at the same temperature and pressure, contain an equal number of molecules.
Mathematical Representation: [ V \propto n ] where ( V ) is the volume and ( n ) is the number of moles.
Example: 1 liter of hydrogen gas and 1 liter of nitrogen gas, at the same temperature and pressure, contain the same number of molecules. This law helps in understanding the molecular composition of gases and is fundamental to the concept of the mole1.
Application in Molar Volume: Avogadro’s law is used to determine the molar volume of gases. At standard temperature and pressure (STP), 1 mole of any gas occupies 22.4 liters.
These laws form the basis of stoichiometry.
Application of “Laws of Chemical Combination” to solve numerical problems:
Applying the laws of chemical combination to solve numerical problems involves understanding the principles behind each law and using them to set up and solve equations. Here are some examples to illustrate how you can apply these laws:
1. Law of Conservation of Mass
Problem: When 10 g of calcium carbonate (CaCO₃) is heated, it decomposes into calcium oxide (CaO) and carbon dioxide (CO₂). If 5.6 g of CaO is formed, what mass of CO₂ is produced?
Solution:
- Write the balanced chemical equation: [ \text{CaCO}_3 \rightarrow \text{CaO} + \text{CO}_2 ]
- Apply the law of conservation of mass: [ \text{Mass of CaCO}_3 = \text{Mass of CaO} + \text{Mass of CO}_2 ]
- Substitute the known values: [ 10 \text{ g} = 5.6 \text{ g} + \text{Mass of CO}_2 ]
- Solve for the mass of CO₂: [ \text{Mass of CO}_2 = 10 \text{ g} - 5.6 \text{ g} = 4.4 \text{ g} ]
2. Law of Definite Proportions
Problem: A sample of pure water is found to contain 2 g of hydrogen and 16 g of oxygen. Verify the law of definite proportions.
Solution:
- Calculate the mass ratio of hydrogen to oxygen: [ \text{Mass ratio} = \frac{\text{Mass of H}}{\text{Mass of O}} = \frac{2 \text{ g}}{16 \text{ g}} = \frac{1}{8} ]
- Compare this ratio with the known ratio for water: The known mass ratio of hydrogen to oxygen in water is 1:8, which matches the calculated ratio, thus verifying the law.
3. Law of Multiple Proportions
Problem: Carbon forms two oxides: CO and CO₂. In CO, 12 g of carbon combines with 16 g of oxygen. In CO₂, 12 g of carbon combines with 32 g of oxygen. Show that these data obey the law of multiple proportions.
Solution:
- Calculate the mass of oxygen per gram of carbon in each compound:
- For CO: [ \frac{16 \text{ g O}}{12 \text{ g C}} = \frac{4}{3} \text{ g O per g C} ]
- For CO₂: [ \frac{32 \text{ g O}}{12 \text{ g C}} = \frac{8}{3} \text{ g O per g C} ]
- Find the ratio of the masses of oxygen that combine with a fixed mass of carbon: [ \frac{\left(\frac{8}{3}\right)}{\left(\frac{4}{3}\right)} = 2 ]
- The ratio is a simple whole number (2:1), confirming the law of multiple proportions.
4. Gay-Lussac’s Law of Gaseous Volumes
Problem: When 2 liters of hydrogen gas react with 1 liter of oxygen gas, how many liters of water vapor are produced?
Solution:
- Write the balanced chemical equation: [ 2\text{H}_2 + \text{O}_2 \rightarrow 2\text{H}_2\text{O} ]
- Apply Gay-Lussac’s law: The volume ratio of hydrogen to oxygen to water vapor is 2:1:2.
- Therefore, 2 liters of hydrogen react with 1 liter of oxygen to produce 2 liters of water vapor.
5. Avogadro’s Law
Problem: If 5 liters of nitrogen gas (N₂) at STP contain (1.34 \times 10^{23}) molecules, how many molecules are there in 10 liters of nitrogen gas at the same conditions?
Solution:
- Use Avogadro’s law, which states that equal volumes of gases at the same temperature and pressure contain an equal number of molecules.
- Set up the proportion: [ \frac{\text{Number of molecules in 5 L}}{\text{Number of molecules in 10 L}} = \frac{5 \text{ L}}{10 \text{ L}} ]
- Solve for the number of molecules in 10 liters: [ \text{Number of molecules in 10 L} = 2 \times 1.34 \times 10^{23} = 2.68 \times 10^{23} ]
By understanding and applying these laws, you can solve a wide range of numerical problems in chemistry.
Real Life Application of Laws of Chemical Combination:
The laws of chemical combination have numerous real-life applications across various fields. Here are some examples:
1. Law of Conservation of Mass
Chemical Manufacturing: In industrial chemical processes, the law of conservation of mass is crucial for designing reactors and ensuring that the input and output masses are balanced. This helps in optimizing the yield and efficiency of chemical reactions.
Environmental Science: This law is used to track pollutants in the environment. For instance, in waste management, the total mass of waste before and after treatment must be accounted for to ensure no mass is lost or unaccounted for.
Cooking: When baking a cake, the total mass of the ingredients (flour, sugar, eggs, etc.) equals the mass of the final baked cake plus any gases released during baking (like CO₂ from baking powder).
2. Law of Definite Proportions
Pharmaceuticals: The law ensures that drugs are manufactured with precise chemical compositions. For example, a specific medication must contain the exact ratio of active ingredients to be effective and safe.
Food Industry: This law is applied in the formulation of food products to maintain consistent taste and quality. For example, table salt (NaCl) always contains sodium and chlorine in a 1:1 ratio by moles.
3. Law of Multiple Proportions
Chemical Synthesis: This law helps chemists understand and predict the formation of different compounds from the same elements. For example, nitrogen and oxygen can form NO, NO₂, N₂O, etc., each with different properties and uses.
Material Science: In the development of new materials, understanding the multiple proportions of elements can lead to the creation of compounds with desired properties, such as different oxides of iron used in various applications.
4. Gay-Lussac’s Law of Gaseous Volumes
Industrial Gas Production: This law is used in the production and storage of industrial gases. For example, in the synthesis of ammonia (NH₃) from nitrogen and hydrogen gases, the volume ratios help in designing reactors and optimizing conditions.
Respiratory Therapy: In medical applications, this law helps in understanding the volumes of gases involved in respiratory treatments, ensuring patients receive the correct mixture of oxygen and other gases.
5. Avogadro’s Law
Chemical Reactions: Avogadro’s law is fundamental in stoichiometry for calculating the volumes of gases involved in reactions. For example, in the Haber process for ammonia production, knowing the volume of nitrogen and hydrogen gases helps in optimizing the reaction conditions.
Balloon Inflation: When inflating balloons with gases like helium, Avogadro’s law helps in determining the amount of gas needed to achieve a desired volume at a given temperature and pressure.
Breathing: The law explains why the volume of air we inhale and exhale remains consistent under the same conditions, which is crucial for understanding lung function and respiratory health.
Industrial Application of Laws of Chemical Combination:
The laws of chemical combination play a crucial role in various industrial processes. Here’s how each law impacts chemical reactions in industry:
1. Law of Conservation of Mass
Industrial Chemical Reactions: This law ensures that all mass inputs are accounted for in the outputs. In industries like pharmaceuticals, petrochemicals, and food processing, precise measurements of reactants and products are essential to maintain efficiency and safety. For example, in the production of sulfuric acid (H₂SO₄) via the Contact Process, the total mass of sulfur dioxide (SO₂), oxygen (O₂), and water (H₂O) must equal the mass of sulfuric acid produced.
Waste Management: Industries use this law to ensure that waste products are minimized and properly accounted for. This is crucial for environmental compliance and sustainability.
2. Law of Definite Proportions
Quality Control: This law is vital in ensuring that compounds are produced with consistent composition. For example, in the pharmaceutical industry, drugs must contain precise amounts of active ingredients to be effective and safe. Any deviation from the fixed ratio can lead to ineffective or harmful products.
Material Consistency: In the production of alloys, such as steel, maintaining a consistent ratio of iron to carbon is essential for achieving the desired properties of the final product.
3. Law of Multiple Proportions
Product Development: This law helps in the development of new compounds with desired properties. For instance, different oxides of nitrogen (NO, NO₂) are used in various applications, from fertilizers to explosives. Understanding the ratios in which elements combine allows chemists to tailor compounds for specific uses.
Chemical Formulation: In industries like cosmetics and food, this law helps in formulating products with precise ingredient ratios to achieve the desired effects and maintain safety standards.
4. Gay-Lussac’s Law of Gaseous Volumes
Gas Production and Storage: This law is used in industries that produce and store gases, such as the production of ammonia (NH₃) in the Haber process. Knowing the volume ratios of nitrogen and hydrogen gases helps in designing efficient reactors and storage systems.
Combustion Processes: In industries like power generation and automotive manufacturing, this law helps in optimizing combustion reactions. For example, the correct volume ratio of air to fuel is crucial for efficient combustion in internal combustion engines.
5. Avogadro’s Law
Gas Measurement: This law is fundamental in industries that deal with gases. For example, in the production of industrial gases like oxygen and nitrogen, Avogadro’s law helps in determining the volumes of gases required and produced.
Chemical Engineering: In processes like the synthesis of polymers, understanding the volume and number of molecules involved helps in scaling up reactions from the laboratory to industrial scale.
Real-Life Industrial Examples
- Ammonia Production (Haber Process): [ \text{N}_2 + 3\text{H}_2 \rightarrow 2\text{NH}_3 ]
- Law of Conservation of Mass: Ensures that the mass of nitrogen and hydrogen gases equals the mass of ammonia produced.
- Gay-Lussac’s Law: Helps in determining the volume ratios of nitrogen and hydrogen gases.
- Sulfuric Acid Production (Contact Process): [ 2\text{SO}_2 + \text{O}_2 \rightarrow 2\text{SO}_3 ] [ \text{SO}_3 + \text{H}_2\text{O} \rightarrow \text{H}_2\text{SO}_4 ]
- Law of Conservation of Mass: Ensures that the mass of sulfur dioxide, oxygen, and water equals the mass of sulfuric acid produced.
- Law of Definite Proportions: Ensures consistent composition of sulfuric acid.
- Steel Manufacturing:
- Law of Definite Proportions: Maintains the precise ratio of iron to carbon to produce steel with desired properties.
These laws are fundamental to the efficiency, safety, and sustainability of industrial chemical processes. They ensure that reactions are predictable, controllable, and scalable, which is essential for industrial applications.
Comments:
Questions based on the laws of chemical combination in JEE Advanced typically test a student’s understanding of fundamental principles and their ability to apply these principles to solve complex problems. Here are some types of questions and examples from past JEE Advanced papers:
Types of Questions
- Conceptual Questions: These questions test the understanding of the basic principles and definitions of the laws.
- Numerical Problems: These involve calculations based on the laws, such as determining the mass of reactants or products.
- Application-Based Questions: These require applying the laws to real-life scenarios or experimental data.
- Multiple Choice Questions (MCQs): These can include single correct answer, multiple correct answers, or assertion-reason type questions.
Examples from Past JEE Advanced Papers
Example 1: Law of Conservation of Mass
Question: When 10 g of calcium carbonate (CaCO₃) is heated, it decomposes into calcium oxide (CaO) and carbon dioxide (CO₂). If 5.6 g of CaO is formed, what mass of CO₂ is produced?
Solution:
- Write the balanced chemical equation: [ \text{CaCO}_3 \rightarrow \text{CaO} + \text{CO}_2 ]
- Apply the law of conservation of mass: [ \text{Mass of CaCO}_3 = \text{Mass of CaO} + \text{Mass of CO}_2 ]
- Substitute the known values: [ 10 \text{ g} = 5.6 \text{ g} + \text{Mass of CO}_2 ]
- Solve for the mass of CO₂: [ \text{Mass of CO}_2 = 10 \text{ g} - 5.6 \text{ g} = 4.4 \text{ g} ]
Example 2: Law of Definite Proportions
Question: A sample of pure water is found to contain 2 g of hydrogen and 16 g of oxygen. Verify the law of definite proportions.
Solution:
- Calculate the mass ratio of hydrogen to oxygen: [ \text{Mass ratio} = \frac{\text{Mass of H}}{\text{Mass of O}} = \frac{2 \text{ g}}{16 \text{ g}} = \frac{1}{8} ]
- Compare this ratio with the known ratio for water: The known mass ratio of hydrogen to oxygen in water is 1:8, which matches the calculated ratio, thus verifying the law.
Example 3: Law of Multiple Proportions
Question: Carbon forms two oxides with oxygen: CO and CO₂. In CO, 12 g of carbon combines with 16 g of oxygen. In CO₂, 12 g of carbon combines with 32 g of oxygen. Show that these data obey the law of multiple proportions.
Solution:
- Calculate the mass of oxygen per gram of carbon in each compound:
- For CO: [ \frac{16 \text{ g O}}{12 \text{ g C}} = \frac{4}{3} \text{ g O per g C} ]
- For CO₂: [ \frac{32 \text{ g O}}{12 \text{ g C}} = \frac{8}{3} \text{ g O per g C} ]
- Find the ratio of the masses of oxygen that combine with a fixed mass of carbon: [ \frac{\left(\frac{8}{3}\right)}{\left(\frac{4}{3}\right)} = 2 ]
- The ratio is a simple whole number (2:1), confirming the law of multiple proportions.
Example 4: Gay-Lussac’s Law of Gaseous Volumes
Question: When 2 liters of hydrogen gas react with 1 liter of oxygen gas, how many liters of water vapor are produced?
Solution:
- Write the balanced chemical equation: [ 2\text{H}_2 + \text{O}_2 \rightarrow 2\text{H}_2\text{O} ]
- Apply Gay-Lussac’s law: The volume ratio of hydrogen to oxygen to water vapor is 2:1:2.
- Therefore, 2 liters of hydrogen react with 1 liter of oxygen to produce 2 liters of water vapor.
Example 5: Avogadro’s Law
Question: If 5 liters of nitrogen gas (N₂) at STP contain (1.34 \times 10^{23}) molecules, how many molecules are there in 10 liters of nitrogen gas at the same conditions?
Solution:
- Use Avogadro’s law, which states that equal volumes of gases at the same temperature and pressure contain an equal number of molecules.
- Set up the proportion: [ \frac{\text{Number of molecules in 5 L}}{\text{Number of molecules in 10 L}} = \frac{5 \text{ L}}{10 \text{ L}} ]
- Solve for the number of molecules in 10 liters: [ \text{Number of molecules in 10 L} = 2 \times 1.34 \times 10^{23} = 2.68 \times 10^{23} ]
These examples illustrate the types of questions you might encounter in JEE Advanced based on the laws of chemical combination. Practicing such problems will help you understand the application of these laws and prepare effectively for the exam.
Atomic and Molecular Masses
Atomic and Molecular Masses
Understanding atomic and molecular masses is fundamental in chemistry, especially for solving problems related to stoichiometry, chemical reactions, and molecular structure. Here’s a detailed overview:
1. Atomic Mass
Definition: Atomic mass (also known as atomic weight) is the mass of an atom, typically expressed in atomic mass units (amu). One atomic mass unit is defined as one-twelfth the mass of a carbon-12 atom.
Atomic Mass Unit (amu):
- 1 amu =\( ( \frac{1}{12} )\) of the mass of a carbon-12 atom.
- 1 amu ≈\( ( 1.660539 \times 10^{-24} )\) grams.
Relative Atomic Mass:
- The relative atomic mass of an element is the weighted average of the masses of its isotopes, based on their natural abundance.
- For example, chlorine has two common isotopes: \(( ^{35}\text{Cl} )\) and \(( ^{37}\text{Cl} )\). The relative atomic mass of chlorine is approximately 35.5 amu.
Calculation Example: \([ \text{Relative Atomic Mass of Cl} = \frac{(75.77 \times 34.969) + (24.23 \times 36.966)}{100} \approx 35.5 \text{ amu} ]\)
2. Molecular Mass
Definition: Molecular mass (or molecular weight) is the sum of the atomic masses of all the atoms in a molecule. It is also expressed in atomic mass units (amu).
Calculation:
- To calculate the molecular mass, sum the atomic masses of all atoms in the molecule.
- For example, the molecular mass of water (H₂O) is calculated as: \([ \text{Molecular Mass of H}_2\text{O} = (2 \times 1.008) + 16.00 = 18.016 \text{ amu} ]\)
Examples:
- Carbon Dioxide (CO₂):\( [ \text{Molecular Mass of CO}_2 = 12.01 + (2 \times 16.00) = 44.01 \text{ amu} ]\)
- Sulfuric Acid (H₂SO₄): \([ \text{Molecular Mass of H}_2\text{SO}_4 = (2 \times 1.008) + 32.07 + (4 \times 16.00) = 98.086 \text{ amu} ]\)
3. Molar Mass
Definition: Molar mass is the mass of one mole of a substance (element or compound) expressed in grams per mole (g/mol). It is numerically equal to the molecular or atomic mass in amu.
Calculation:
- For elements, the molar mass is the atomic mass in grams.
- For compounds, the molar mass is the sum of the atomic masses of all atoms in the molecule, expressed in grams per mole.
Examples:
- Oxygen (O₂): \([ \text{Molar Mass of O}_2 = 2 \times 16.00 \text{ g/mol} = 32.00 \text{ g/mol} ]\)
- Glucose (C₆H₁₂O₆): \([ \text{Molar Mass of C}6\text{H}{12}\text{O}_6 = (6 \times 12.01) + (12 \times 1.008) + (6 \times 16.00) = 180.16 \text{ g/mol} ]\)
4. Applications in Stoichiometry
Balancing Chemical Equations:
- Atomic and molecular masses are used to balance chemical equations by ensuring the mass of reactants equals the mass of products.
Example: \([ \text{C}_3\text{H}_8 + 5\text{O}_2 \rightarrow 3\text{CO}_2 + 4\text{H}_2\text{O} ]\)
- Calculate the molar masses:
- Propane (C₃H₈): \(( 3 \times 12.01 + 8 \times 1.008 = 44.094 \text{ g/mol} )\)
- Oxygen (O₂): \(( 2 \times 16.00 = 32.00 \text{ g/mol} )\)
- Carbon Dioxide (CO₂): \(( 12.01 + 2 \times 16.00 = 44.01 \text{ g/mol} )\)
- Water (H₂O): \(( 2 \times 1.008 + 16.00 = 18.016 \text{ g/mol} )\)
Using Molar Mass in Calculations:
- To find the amount of a substance in moles, use the formula: \([ \text{Number of moles} = \frac{\text{Mass of substance (g)}}{\text{Molar mass (g/mol)}} ]\)
Example:
- Calculate the number of moles in 88 g of CO₂: \([ \text{Number of moles} = \frac{88 \text{ g}}{44.01 \text{ g/mol}} \approx 2 \text{ moles} ]\)
5. Isotopes and Average Atomic Mass
Isotopes:
- Atoms of the same element with different numbers of neutrons and hence different masses.
- Example: Carbon has isotopes \(( ^{12}\text{C} )\), \(( ^{13}\text{C} )\), and \(( ^{14}\text{C} )\).
Average Atomic Mass:
- Calculated based on the relative abundance of each isotope.
- Example: Chlorine has isotopes \(( ^{35}\text{Cl} )\) and \(( ^{37}\text{Cl} )\) with average atomic mass ≈ 35.5 amu.
6. Practical Applications
Chemical Reactions:
- Determining reactant and product masses.
- Example: In the reaction of hydrogen and oxygen to form water, knowing the molar masses helps in calculating the required amounts of each reactant.
Pharmaceuticals:
- Accurate calculation of dosages based on molar masses of active ingredients.
Environmental Science:
- Tracking pollutants and their reactions in the environment.
Summary
Understanding atomic and molecular masses is essential for solving problems in stoichiometry, balancing chemical equations, and performing various calculations in chemistry
Additional Applications of Atomic and Molecular Mass
The concepts of atomic and molecular mass are used in various fields beyond basic chemistry. Here are some additional areas where these concepts are crucial:
- Biochemistry:
- Protein and DNA Analysis: Determining the molecular masses of proteins and nucleic acids helps in understanding their structure and function. Techniques like mass spectrometry are used to analyze the molecular masses of biomolecules.
- Enzyme Kinetics: Calculating the molecular masses of substrates and products is essential for studying enzyme-catalyzed reactions.
- Pharmacology:
- Drug Design: Molecular mass is a critical factor in the design and synthesis of pharmaceutical compounds. It influences the drug’s absorption, distribution, metabolism, and excretion (ADME) properties.
- Dosage Calculations: Accurate dosage formulations depend on the precise molecular mass of the active ingredients.
- Environmental Science:
- Pollutant Tracking: Understanding the molecular masses of pollutants helps in monitoring and controlling their distribution in the environment.
- Atmospheric Chemistry: Molecular masses are used to study the composition and reactions of atmospheric gases, which is crucial for understanding climate change and air quality.
- Material Science:
- Polymer Chemistry: The molecular mass of polymers determines their physical properties, such as strength, elasticity, and melting point.
- Nanotechnology: Atomic and molecular masses are important in the synthesis and characterization of nanomaterials.
Real-Life Examples
- Medical Diagnostics:
- Mass Spectrometry: Used to determine the molecular mass of biomolecules in blood samples, aiding in the diagnosis of diseases.
- MRI Contrast Agents: The molecular mass of contrast agents affects their distribution and effectiveness in imaging.
- Food Industry:
- Nutritional Analysis: Determining the molecular masses of vitamins, minerals, and other nutrients helps in formulating balanced diets and supplements.
- Food Additives: The molecular mass of additives influences their behavior and stability in food products.
- Agriculture:
- Fertilizers: The molecular mass of compounds like ammonium nitrate (NH₄NO₃) is used to calculate the required amounts for optimal crop growth.
- Pesticides: Understanding the molecular mass helps in determining the dosage and environmental impact of pesticides.
Industrial Usage
- Chemical Manufacturing:
- Synthesis of Chemicals: Accurate molecular masses are essential for the synthesis of chemicals in industries. For example, in the production of sulfuric acid (H₂SO₄), knowing the molecular masses of reactants and products ensures efficient and safe production.
- Quality Control: Ensuring that products meet specified molecular mass criteria is crucial for maintaining quality standards.
- Pharmaceutical Industry:
- Drug Development: Molecular mass is a key parameter in the development and testing of new drugs. It affects the drug’s pharmacokinetics and pharmacodynamics.
- Formulation: The molecular mass of active pharmaceutical ingredients (APIs) is used to formulate drugs with the correct dosage and efficacy.
- Petrochemical Industry:
- Refining Processes: Molecular masses of hydrocarbons are used to optimize refining processes and produce fuels with desired properties.
- Polymer Production: The molecular mass of monomers determines the properties of the resulting polymers, which are used in various applications from plastics to textiles.
- Environmental Monitoring:
- Air and Water Quality: Monitoring the molecular masses of pollutants helps in assessing and controlling environmental pollution.
- Waste Management: Understanding the molecular masses of waste components aids in developing effective treatment and recycling processes.
These examples illustrate the wide-ranging applications of atomic and molecular masses in various fields, highlighting their importance in both scientific research and industrial processes. If you have any specific questions or need further details, feel free to ask!
Mole Concept and Molar Masses
Mole Concept and Molar Masses
Understanding the mole concept and molar masses is crucial for solving problems in stoichiometry, chemical reactions, and quantitative analysis in chemistry. Here’s a detailed overview:
1. Mole Concept
Definition: The mole is a fundamental unit in chemistry that represents a specific number of particles (atoms, molecules, ions, etc.). One mole of any substance contains exactly \(( 6.02214076 \times 10^{23} )\) elementary entities, known as Avogadro’s number.
Avogadro’s Number: \([ N_A = 6.02214076 \times 10^{23} ]\)
Mole and Mass Relationship:
- The mass of one mole of a substance in grams is equal to its molar mass.
- For example, one mole of carbon-12 atoms has a mass of exactly 12 grams.
Calculating Moles: \([ \text{Number of moles} = \frac{\text{Mass of substance (g)}}{\text{Molar mass (g/mol)}} ]\)
Example:
- Calculate the number of moles in 88 g of carbon dioxide (CO₂): \([ \text{Molar mass of CO}_2 = 12.01 + (2 \times 16.00) = 44.01 \text{ g/mol} ] [ \text{Number of moles} = \frac{88 \text{ g}}{44.01 \text{ g/mol}} \approx 2 \text{ moles} ]\)
2. Molar Mass
Definition: Molar mass is the mass of one mole of a substance (element or compound) expressed in grams per mole (g/mol). It is numerically equal to the molecular or atomic mass in atomic mass units (amu).
Calculation:
- For elements, the molar mass is the atomic mass in grams.
- For compounds, the molar mass is the sum of the atomic masses of all atoms in the molecule, expressed in grams per mole.
Examples:
- Oxygen (O₂): \([ \text{Molar Mass of O}_2 = 2 \times 16.00 \text{ g/mol} = 32.00 \text{ g/mol} ]\)
- Glucose (C₆H₁₂O₆): \([ \text{Molar Mass of C}6\text{H}{12}\text{O}_6 = (6 \times 12.01) + (12 \times 1.008) + (6 \times 16.00) = 180.16 \text{ g/mol} ]\)
3. Applications in Stoichiometry
Balancing Chemical Equations:
- Molar masses are used to balance chemical equations by ensuring the mass of reactants equals the mass of products.
Example: \([ \text{C}_3\text{H}_8 + 5\text{O}_2 \rightarrow 3\text{CO}_2 + 4\text{H}_2\text{O} ]\)
- Calculate the molar masses:
- Propane (C₃H₈): \(( 3 \times 12.01 + 8 \times 1.008 = 44.094 \text{ g/mol} )\)
- Oxygen (O₂): \(( 2 \times 16.00 = 32.00 \text{ g/mol} )\)
- Carbon Dioxide (CO₂): \(( 12.01 + 2 \times 16.00 = 44.01 \text{ g/mol} )\)
- Water (H₂O): \(( 2 \times 1.008 + 16.00 = 18.016 \text{ g/mol} )\)
Using Molar Mass in Calculations:
- To find the amount of a substance in moles, use the formula: \([ \text{Number of moles} = \frac{\text{Mass of substance (g)}}{\text{Molar mass (g/mol)}} ]\)
Example:
- Calculate the number of moles in 88 g of CO₂: \([ \text{Number of moles} = \frac{88 \text{ g}}{44.01 \text{ g/mol}} \approx 2 \text{ moles} ]\)
4. Concentration Terms
Molarity (M):
- Molarity is the number of moles of solute per liter of solution. \([ \text{Molarity (M)} = \frac{\text{Number of moles of solute}}{\text{Volume of solution in liters}} ]\)
Example:
- Calculate the molarity of a solution containing 5 moles of NaCl in 2 liters of solution: \([ \text{Molarity} = \frac{5 \text{ moles}}{2 \text{ L}} = 2.5 \text{ M} ]\)
Molality (m):
- Molality is the number of moles of solute per kilogram of solvent. \([ \text{Molality (m)} = \frac{\text{Number of moles of solute}}{\text{Mass of solvent in kg}} ]\)
Example:
- Calculate the molality of a solution containing 3 moles of KCl in 1 kg of water: \([ \text{Molality} = \frac{3 \text{ moles}}{1 \text{ kg}} = 3 \text{ m} ]\)
5. Empirical and Molecular Formulas
Empirical Formula:
- The empirical formula represents the simplest whole-number ratio of atoms in a compound.
Example:
- The empirical formula of glucose (C₆H₁₂O₆) is CH₂O.
Molecular Formula:
- The molecular formula represents the actual number of atoms of each element in a molecule.
Example:
- The molecular formula of glucose is C₆H₁₂O₆.
Determining Molecular Formula:
- To determine the molecular formula, divide the molar mass of the compound by the molar mass of the empirical formula. \([ \text{Molecular Formula} = (\text{Empirical Formula})_n ] [ n = \frac{\text{Molar mass of compound}}{\text{Molar mass of empirical formula}} ]\)
Example:
- If the molar mass of a compound is 180 g/mol and its empirical formula is CH₂O (molar mass = 30 g/mol):\( [ n = \frac{180 \text{ g/mol}}{30 \text{ g/mol}} = 6 ]\)
- Therefore, the molecular formula is ( (CH₂O)_6 = C₆H₁₂O₆ ).
6. Practical Applications
Chemical Reactions:
- Determining reactant and product masses.
- Example: In the reaction of hydrogen and oxygen to form water, knowing the molar masses helps in calculating the required amounts of each reactant.
Pharmaceuticals:
- Accurate calculation of dosages based on molar masses of active ingredients.
Environmental Science:
- Tracking pollutants and their reactions in the environment.
Additional Applications of Mole Concept and Molar Mass
The concepts of mole and molar mass are used in various fields beyond basic chemistry. Here are some additional areas where these concepts are crucial:
- Biochemistry:
- Protein and DNA Analysis: Determining the molecular masses of proteins and nucleic acids helps in understanding their structure and function. Techniques like mass spectrometry are used to analyze the molecular masses of biomolecules.
- Enzyme Kinetics: Calculating the molecular masses of substrates and products is essential for studying enzyme-catalyzed reactions.
- Pharmacology:
- Drug Design: Molecular mass is a critical factor in the design and synthesis of pharmaceutical compounds. It influences the drug’s absorption, distribution, metabolism, and excretion (ADME) properties.
- Dosage Calculations: Accurate dosage formulations depend on the precise molecular mass of the active ingredients.
- Environmental Science:
- Pollutant Tracking: Understanding the molecular masses of pollutants helps in monitoring and controlling their distribution in the environment.
- Atmospheric Chemistry: Molecular masses are used to study the composition and reactions of atmospheric gases, which is crucial for understanding climate change and air quality.
- Material Science:
- Polymer Chemistry: The molecular mass of polymers determines their physical properties, such as strength, elasticity, and melting point.
- Nanotechnology: Atomic and molecular masses are important in the synthesis and characterization of nanomaterials.
Real-Life Examples
- Medical Diagnostics:
- Mass Spectrometry: Used to determine the molecular mass of biomolecules in blood samples, aiding in the diagnosis of diseases.
- MRI Contrast Agents: The molecular mass of contrast agents affects their distribution and effectiveness in imaging.
- Food Industry:
- Nutritional Analysis: Determining the molecular masses of vitamins, minerals, and other nutrients helps in formulating balanced diets and supplements.
- Food Additives: The molecular mass of additives influences their behavior and stability in food products.
- Agriculture:
- Fertilizers: The molecular mass of compounds like ammonium nitrate (NH₄NO₃) is used to calculate the required amounts for optimal crop growth.
- Pesticides: Understanding the molecular mass helps in determining
Percentage Composition
Percentage Composition
Percentage composition is a fundamental concept in chemistry that describes the relative mass of each element in a compound. It is essential for understanding the composition of compounds and is widely used in stoichiometry, chemical analysis, and various industrial applications. Here’s a detailed overview:
1. Definition
Percentage Composition: The percentage composition of a compound is the ratio of the mass of each element to the total mass of the compound, multiplied by 100.
\([ \text{Percentage Composition of Element} = \left( \frac{\text{Mass of Element in Compound}}{\text{Total Mass of Compound}} \right) \times 100 ]\)
2. Calculation of Percentage Composition
To calculate the percentage composition of an element in a compound, follow these steps:
- Determine the Molar Mass of the Compound:
- Sum the atomic masses of all atoms in the compound to find the molar mass.
- Calculate the Mass of Each Element:
- Multiply the atomic mass of each element by the number of atoms of that element in the compound.
- Calculate the Percentage Composition:
- Use the formula to find the percentage composition of each element.
Example: Calculate the percentage composition of water (H₂O).
- Molar Mass of H₂O: \([ \text{Molar Mass of H}_2\text{O} = (2 \times 1.008) + 16.00 = 18.016 \text{ g/mol} ]\)
- Mass of Hydrogen:\( [ \text{Mass of H} = 2 \times 1.008 = 2.016 \text{ g} ]\)
- Mass of Oxygen: \([ \text{Mass of O} = 16.00 \text{ g} ]\)
- Percentage Composition: \([ \text{Percentage of H} = \left( \frac{2.016}{18.016} \right) \times 100 \approx 11.19% ] [ \text{Percentage of O} = \left( \frac{16.00}{18.016} \right) \times 100 \approx 88.81% ]\)
3. Empirical and Molecular Formulas
Empirical Formula: The empirical formula represents the simplest whole-number ratio of atoms in a compound.
Molecular Formula: The molecular formula represents the actual number of atoms of each element in a molecule.
Determining Empirical Formula:
- Convert the percentage composition to grams (assuming 100 g of the compound).
- Convert grams to moles using the atomic masses.
- Divide the moles of each element by the smallest number of moles to find the simplest ratio.
- Write the empirical formula based on the simplest ratio.
Example: A compound contains 40% carbon, 6.67% hydrogen, and 53.33% oxygen by mass. Determine its empirical formula.
- Convert to Grams: \([ \text{C} = 40 \text{ g}, \text{H} = 6.67 \text{ g}, \text{O} = 53.33 \text{ g} ]\)
- Convert to Moles: \([ \text{Moles of C} = \frac{40}{12.01} \approx 3.33 ] [ \text{Moles of H} = \frac{6.67}{1.008} \approx 6.62 ] [ \text{Moles of O} = \frac{53.33}{16.00} \approx 3.33 ]\)
- Simplest Ratio: \([ \text{C} : \text{H} : \text{O} = \frac{3.33}{3.33} : \frac{6.62}{3.33} : \frac{3.33}{3.33} = 1 : 2 : 1 ]\)
- Empirical Formula: \([ \text{CH}_2\text{O} ]\)
4. Practical Applications
Chemical Analysis:
- Determining the composition of unknown compounds.
- Verifying the purity of substances.
Pharmaceuticals:
- Formulating drugs with precise compositions.
- Ensuring the correct dosage of active ingredients.
Environmental Science:
- Analyzing pollutants and their compositions.
- Monitoring the composition of atmospheric gases.
5. Industrial Applications
Chemical Manufacturing:
- Ensuring the correct composition of reactants and products.
- Quality control in the production of chemicals.
Food Industry:
- Determining the nutritional content of food products.
- Ensuring the correct composition of additives and preservatives.
Agriculture:
- Formulating fertilizers with specific nutrient compositions.
- Analyzing soil composition to optimize crop growth.
Summary
Understanding percentage composition is essential for analyzing and verifying the composition of compounds. It is widely used in various fields, including chemical analysis, pharmaceuticals, environmental science, and industrial applications.
Stoichiometry and Stoichiometric Calculations
Stoichiometry and Stoichiometric Calculations
Stoichiometry is a branch of chemistry that deals with the quantitative relationships between the reactants and products in a chemical reaction. It is essential for understanding how much of each substance is involved in a reaction and for predicting the amounts of products formed. Here’s a detailed overview:
1. Definition
Stoichiometry: The calculation of reactants and products in chemical reactions using the balanced chemical equation.
2. Stoichiometric Coefficients
Stoichiometric Coefficients: The numbers in front of the chemical formulas in a balanced chemical equation. They indicate the relative amounts of reactants and products.
Example: \([ \text{C}_3\text{H}_8 + 5\text{O}_2 \rightarrow 3\text{CO}_2 + 4\text{H}_2\text{O} ]\)
- The coefficients are 1 for \((\text{C}_3\text{H}_8)\), 5 for \((\text{O}_2)\), 3 for \((\text{CO}_2)\), and 4 for \((\text{H}_2\text{O})\).
3. Mole Concept in Stoichiometry
Mole Concept: One mole of any substance contains \(( 6.022 \times 10^{23} )\) entities (atoms, molecules, ions, etc.), known as Avogadro’s number.
Molar Mass: The mass of one mole of a substance, expressed in grams per mole (g/mol).
Example:
- Molar mass of \((\text{H}_2\text{O}): [ \text{Molar Mass of H}_2\text{O} = (2 \times 1.008) + 16.00 = 18.016 \text{ g/mol} ]\)
4. Balancing Chemical Equations
Balancing Equations: Ensuring that the number of atoms of each element is the same on both sides of the equation.
Steps to Balance Equations:
- Write the unbalanced equation.
- Count the number of atoms of each element on both sides.
- Adjust the coefficients to balance the atoms.
- Check that all atoms are balanced.
Example: \([ \text{Fe} + \text{O}_2 \rightarrow \text{Fe}_2\text{O}_3 ] Balanced: [ 4\text{Fe} + 3\text{O}_2 \rightarrow 2\text{Fe}_2\text{O}_3 ]\)
5. Stoichiometric Calculations
Using Moles in Calculations:
- To find the amount of a substance in moles: \([ \text{Number of moles} = \frac{\text{Mass of substance (g)}}{\text{Molar mass (g/mol)}} ]\)
Example:
- Calculate the number of moles in 88 g of (\(\text{CO}_2): [ \text{Molar mass of CO}_2 = 12.01 + (2 \times 16.00) = 44.01 \text{ g/mol} ] [ \text{Number of moles} = \frac{88 \text{ g}}{44.01 \text{ g/mol}} \approx 2 \text{ moles} ]\)
Using Stoichiometric Ratios:
- Use the coefficients from the balanced equation to find the ratio of reactants to products.
Example: \([ \text{C}_3\text{H}_8 + 5\text{O}_2 \rightarrow 3\text{CO}_2 + 4\text{H}_2\text{O} ]\)
- 1 mole of \((\text{C}_3\text{H}_8)\) reacts with 5 moles of \((\text{O}_2)\) to produce 3 moles of \((\text{CO}_2)\) and 4 moles of \((\text{H}_2\text{O})\).
6. Limiting Reactant and Excess Reactant
Limiting Reactant: The reactant that is completely consumed in a reaction, limiting the amount of product formed.
Excess Reactant: The reactant that is not completely consumed in a reaction.
Steps to Identify Limiting Reactant:
- Calculate the moles of each reactant.
- Use the stoichiometric ratios to determine which reactant will be consumed first.
Example: \([ \text{N}_2 + 3\text{H}_2 \rightarrow 2\text{NH}_3 ]\)
- If you have 1 mole of \((\text{N}_2)\) and 3 moles of \((\text{H}_2)\), \((\text{N}_2)\) is the limiting reactant.
7. Yield Calculations
Theoretical Yield: The maximum amount of product that can be formed from the given amounts of reactants.
Actual Yield: The amount of product actually obtained from a reaction.
Percent Yield: \([ \text{Percent Yield} = \left( \frac{\text{Actual Yield}}{\text{Theoretical Yield}} \right) \times 100 ]\)
Example:
- If the theoretical yield of \((\text{NH}_3)\) is 34 g and the actual yield is 30 g: \([ \text{Percent Yield} = \left( \frac{30 \text{ g}}{34 \text{ g}} \right) \times 100 \approx 88.24% ]\)
8. Practical Applications
Chemical Manufacturing:
- Ensuring the correct proportions of reactants to maximize yield and minimize waste.
Pharmaceuticals:
- Formulating drugs with precise amounts of active ingredients.
Environmental Science:
- Analyzing pollutant levels and their reactions in the environment.
Summary
Stoichiometry and stoichiometric calculations are essential for understanding and predicting the outcomes of chemical reactions.
Concentration of Solutions
Concentration of Solutions
Concentration of solutions is a crucial concept in chemistry that describes the amount of solute present in a given quantity of solvent or solution. Understanding this concept is essential for solving problems related to solution chemistry, stoichiometry, and various industrial applications. Here’s a detailed overview:
1. Definition
Concentration: The amount of solute present in a given quantity of solvent or solution.
2. Ways to Express Concentration
There are several ways to express the concentration of a solution, each useful for different types of calculations and applications:
a. Molarity (M)
Definition: Molarity is the number of moles of solute per liter of solution.
\([ \text{Molarity (M)} = \frac{\text{Number of moles of solute}}{\text{Volume of solution in liters}} ]\)
Example:
- Calculate the molarity of a solution containing 5 moles of NaCl in 2 liters of solution: \([ \text{Molarity} = \frac{5 \text{ moles}}{2 \text{ L}} = 2.5 \text{ M} ]\)
b. Molality (m)
Definition: Molality is the number of moles of solute per kilogram of solvent.
\([ \text{Molality (m)} = \frac{\text{Number of moles of solute}}{\text{Mass of solvent in kg}} ]\)
Example:
- Calculate the molality of a solution containing 3 moles of KCl in 1 kg of water: \([ \text{Molality} = \frac{3 \text{ moles}}{1 \text{ kg}} = 3 \text{ m} ]\)
c. Mole Fraction (χ)
Definition: Mole fraction is the ratio of the number of moles of a component to the total number of moles of all components in the solution.
\([ \text{Mole Fraction (χ)} = \frac{\text{Number of moles of component}}{\text{Total number of moles of all components}} ]\)
Example:
- Calculate the mole fraction of NaCl in a solution containing 2 moles of NaCl and 8 moles of water: \([ \text{Mole Fraction of NaCl} = \frac{2}{2 + 8} = 0.2 ]\)
d. Mass Percent (Weight Percent)
Definition: Mass percent is the mass of solute divided by the total mass of the solution, multiplied by 100.
\([ \text{Mass Percent} = \left( \frac{\text{Mass of solute}}{\text{Total mass of solution}} \right) \times 100 ]\)
Example:
- Calculate the mass percent of NaCl in a solution containing 10 g of NaCl and 90 g of water:\( [ \text{Mass Percent} = \left( \frac{10 \text{ g}}{10 \text{ g} + 90 \text{ g}} \right) \times 100 = 10% ]\)
e. Volume Percent
Definition: Volume percent is the volume of solute divided by the total volume of the solution, multiplied by 100.
\([ \text{Volume Percent} = \left( \frac{\text{Volume of solute}}{\text{Total volume of solution}} \right) \times 100 ]\)
Example:
- Calculate the volume percent of ethanol in a solution containing 30 mL of ethanol and 70 mL of water: \([ \text{Volume Percent} = \left( \frac{30 \text{ mL}}{30 \text{ mL} + 70 \text{ mL}} \right) \times 100 = 30% ]\)
3. Dilution of Solutions
Dilution: The process of reducing the concentration of a solute in a solution, usually by adding more solvent.
Dilution Formula: \([ M_1 V_1 = M_2 V_2 ]\) where \(( M_1 )\) and \(( M_2 )\) are the initial and final molarities, and \(( V_1 )\) and \(( V_2 )\) are the initial and final volumes.
Example:
- To dilute 1 L of a 2 M NaCl solution to 0.5 M: \([ 2 \text{ M} \times 1 \text{ L} = 0.5 \text{ M} \times V_2 ] [ V_2 = \frac{2 \text{ M} \times 1 \text{ L}}{0.5 \text{ M}} = 4 \text{ L} ]\)
- Therefore, add 3 L of water to the original solution.
4. Practical Applications
Chemical Reactions:
- Calculating reactant and product concentrations.
- Example: In titrations, the concentration of an unknown solution is determined by reacting it with a solution of known concentration.
Pharmaceuticals:
- Formulating drugs with precise concentrations.
- Ensuring the correct dosage of active ingredients.
Environmental Science:
- Analyzing pollutant concentrations in air and water.
- Monitoring the concentration of nutrients in soil.
5. Industrial Applications
Chemical Manufacturing:
- Ensuring the correct concentration of reactants and products.
- Quality control in the production of chemicals.
Food Industry:
- Determining the concentration of additives and preservatives.
- Ensuring the correct concentration of nutrients in food products.
Agriculture:
- Formulating fertilizers with specific nutrient concentrations.
- Analyzing soil and water concentrations to optimize crop growth.
Summary
Understanding the concentration of solutions is essential for analyzing and controlling the composition of solutions in various fields. It is widely used in chemical reactions, pharmaceuticals, environmental science, and industrial applications.
Limiting Reagent
Limiting Reagent
The concept of the limiting reagent is crucial in stoichiometry and chemical reactions. It helps determine the amount of product formed in a reaction and identifies which reactant will be completely consumed first. Here’s a detailed overview:
1. Definition
Limiting Reagent: The reactant that is completely consumed in a chemical reaction, limiting the amount of product formed. It determines the maximum amount of product that can be produced.
Excess Reagent: The reactant that is not completely consumed in a reaction and remains after the reaction is complete.
2. Identifying the Limiting Reagent
To identify the limiting reagent in a chemical reaction, follow these steps:
- Write the Balanced Chemical Equation:
- Ensure the chemical equation is balanced with the correct stoichiometric coefficients.
- Calculate the Moles of Each Reactant:
- Convert the masses of reactants to moles using their molar masses.
- Use Stoichiometric Ratios:
- Compare the mole ratio of the reactants with the stoichiometric ratio from the balanced equation.
- Determine the Limiting Reagent:
- The reactant that produces the least amount of product is the limiting reagent.
Example: Consider the reaction between hydrogen and oxygen to form water:\( [ 2\text{H}_2 + \text{O}_2 \rightarrow 2\text{H}_2\text{O} ]\)
Suppose we have 10 moles of \((\text{H}_2) and 7 moles of (\text{O}_2)\).
- Balanced Equation: \([ 2\text{H}_2 + \text{O}_2 \rightarrow 2\text{H}_2\text{O} ]\)
- Calculate Moles:
- Moles of \( (\text{H}_2)\) = 10
- Moles of \((\text{O}_2)\) = 7
- Stoichiometric Ratios:
- According to the balanced equation, 2 moles of \((\text{H}_2)\) react with 1 mole of \((\text{O}_2)\).
- Determine Limiting Reagent:
- For 10 moles of \((\text{H}_2)\), we need \(( \frac{10}{2} = 5 )\) moles of \((\text{O}_2)\).
- Since we have 7 moles of \((\text{O}_2)\), which is more than required, \((\text{H}_2)\) is the limiting reagent.
3. Calculating the Amount of Product
Once the limiting reagent is identified, use it to calculate the amount of product formed.
Example: Using the previous example, calculate the amount of water \(((\text{H}_2\text{O}))\) formed.
- Balanced Equation: \([ 2\text{H}_2 + \text{O}_2 \rightarrow 2\text{H}_2\text{O} ]\)
- Limiting Reagent:
- \((\text{H}_2)\) is the limiting reagent.
- Calculate Moles of Product:
- According to the balanced equation, 2 moles of \((\text{H}_2)\) produce 2 moles of \((\text{H}_2\text{O})\).
- Therefore, 10 moles of \((\text{H}_2)\) will produce 10 moles of \((\text{H}_2\text{O})\).
4. Practical Applications
Chemical Manufacturing:
- Ensuring the correct proportions of reactants to maximize yield and minimize waste.
Pharmaceuticals:
- Formulating drugs with precise amounts of active ingredients.
Environmental Science:
- Analyzing pollutant levels and their reactions in the environment.
5. Industrial Applications
Chemical Manufacturing:
- Optimizing the use of raw materials by identifying the limiting reagent.
- Reducing costs by minimizing excess reactants.
Food Industry:
- Ensuring the correct proportions of ingredients in food products.
- Optimizing the production process to reduce waste.
Agriculture:
- Formulating fertilizers with specific nutrient compositions.
- Analyzing soil composition to optimize crop growth.
Summary
Understanding the concept of the limiting reagent is essential for predicting the outcomes of chemical reactions and optimizing the use of reactants. It is widely used in chemical manufacturing, pharmaceuticals, environmental science, and various industrial applications.
Empirical and Molecular Formulas
Empirical and Molecular Formulas
Understanding empirical and molecular formulas is essential for determining the composition of compounds and solving problems in stoichiometry. Here’s a detailed overview:
1. Definitions
Empirical Formula: The empirical formula of a compound gives the simplest whole-number ratio of the atoms of each element present in the compound.
Molecular Formula: The molecular formula of a compound gives the actual number of atoms of each element present in a molecule of the compound. It is a multiple of the empirical formula.
2. Determining Empirical Formula
To determine the empirical formula of a compound, follow these steps:
- Write the Percent Composition:
- Convert the percentage composition of each element to grams (assuming 100 g of the compound).
- Convert to Moles:
- Divide the mass of each element by its atomic mass to find the number of moles.
- Find the Simplest Ratio:
- Divide the number of moles of each element by the smallest number of moles to get the simplest whole-number ratio.
- Write the Empirical Formula:
- Use the simplest ratio to write the empirical formula.
Example: A compound contains 40% carbon, 6.67% hydrogen, and 53.33% oxygen by mass. Determine its empirical formula.
- Convert to Grams: \( [ \text{C} = 40 \text{ g}, \text{H} = 6.67 \text{ g}, \text{O} = 53.33 \text{ g} ]\)
- Convert to Moles: \([ \text{Moles of C} = \frac{40}{12.01} \approx 3.33 ] [ \text{Moles of H} = \frac{6.67}{1.008} \approx 6.62 ] [ \text{Moles of O} = \frac{53.33}{16.00} \approx 3.33 ]\)
- Simplest Ratio: \([ \text{C} : \text{H} : \text{O} = \frac{3.33}{3.33} : \frac{6.62}{3.33} : \frac{3.33}{3.33} = 1 : 2 : 1 ]\)
- Empirical Formula: \([ \text{CH}_2\text{O} ]\)
3. Determining Molecular Formula
To determine the molecular formula, follow these steps:
- Determine the Empirical Formula:
- Follow the steps outlined above to find the empirical formula.
- Calculate the Empirical Formula Mass:
- Sum the atomic masses of all atoms in the empirical formula.
- Determine the Molar Mass:
- Obtain the molar mass of the compound (usually given in the problem).
- Find the Multiplication Factor:
- Divide the molar mass by the empirical formula mass to find the multiplication factor \(( n )\).
- Write the Molecular Formula:
- Multiply the subscripts in the empirical formula by the multiplication factor to get the molecular formula.
Example: The empirical formula of a compound is \(( \text{CH}_2\text{O} )\) and its molar mass is 180 g/mol. Determine the molecular formula.
- Empirical Formula: \([ \text{CH}_2\text{O} ]\)
- Empirical Formula Mass: \([ \text{C} = 12.01, \text{H} = 1.008 \times 2, \text{O} = 16.00 ] [ \text{Empirical Formula Mass} = 12.01 + 2 \times 1.008 + 16.00 = 30.026 \text{ g/mol} ]\)
- Molar Mass: \([ 180 \text{ g/mol} ]\)
- Multiplication Factor: \([ n = \frac{180 \text{ g/mol}}{30.026 \text{ g/mol}} \approx 6 ]\)
- Molecular Formula: \([ (\text{CH}_2\text{O})_6 = \text{C}6\text{H}{12}\text{O}_6 ]\)
4. Practical Applications
Chemical Analysis:
- Determining the composition of unknown compounds.
- Verifying the purity of substances.
Pharmaceuticals:
- Formulating drugs with precise compositions.
- Ensuring the correct dosage of active ingredients.
Environmental Science:
- Analyzing pollutants and their compositions.
- Monitoring the composition of atmospheric gases.
5. Industrial Applications
Chemical Manufacturing:
- Ensuring the correct composition of reactants and products.
- Quality control in the production of chemicals.
Food Industry:
- Determining the nutritional content of food products.
- Ensuring the correct composition of additives and preservatives.
Agriculture:
- Formulating fertilizers with specific nutrient compositions.
- Analyzing soil composition to optimize crop growth.
Summary
Understanding empirical and molecular formulas is essential for analyzing and verifying the composition of compounds. It is widely used in chemical analysis, pharmaceuticals, environmental science, and industrial applications.
Avogadro's Law
Avogadro’s Law
Definition: Avogadro’s Law states that the volume of a gas is directly proportional to the number of moles of the gas, provided the temperature and pressure remain constant. Mathematically, it is expressed as: \([ V \propto n ]\) or \([ \frac{V}{n} = k ]\) where ( V ) is the volume of the gas, ( n ) is the number of moles, and ( k ) is a constant.
Formula: \([ \frac{V_1}{n_1} = \frac{V_2}{n_2} ]\) This equation shows that if the amount of gas changes, the volume changes proportionally, assuming constant temperature and pressure.
Graphical Representation: A graph of volume (( V )) versus the number of moles (( n )) at constant temperature and pressure is a straight line passing through the origin, indicating direct proportionality.
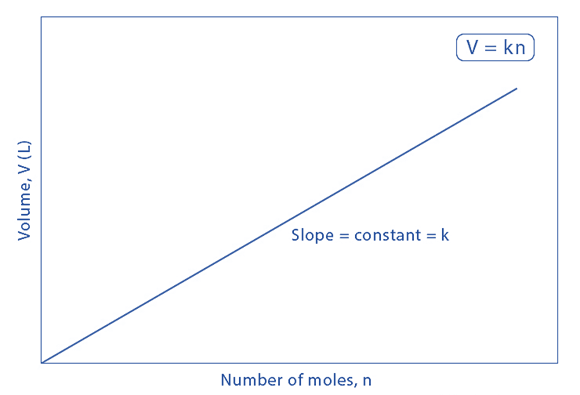
Derivation from Ideal Gas Law
The ideal gas law is given by: [ PV = nRT ] where ( P ) is the pressure, ( V ) is the volume, ( n ) is the number of moles, ( R ) is the universal gas constant, and ( T ) is the temperature.
At constant ( P ) and ( T ): \([ V = \frac{nRT}{P} ]\) Since \(( \frac{RT}{P} )\) is a constant, we can write: \([ V \propto n ]\)
Molar Volume
At standard temperature and pressure (STP: 0°C and 1 atm), one mole of any gas occupies 22.4 liters. This is known as the molar volume of a gas.
Real-Life Examples
- Breathing: Human lungs expand and contract based on the volume of air (gas) inhaled and exhaled. The volume of air in the lungs changes with the number of moles of air, demonstrating Avogadro’s Law.
- Balloons: When you blow up a balloon, the volume increases as more air (moles of gas) is added, assuming temperature and pressure are constant.
Industrial Applications
- Chemical Manufacturing: In industries where gases are used as reactants, understanding the relationship between volume and moles helps in scaling reactions. For example, in the production of ammonia via the Haber process, precise volumes of nitrogen and hydrogen gases are required.
- Gas Storage: Industries that store gases (like oxygen or nitrogen) in cylinders use Avogadro’s Law to determine the amount of gas in a container based on its volume.
- Pharmaceuticals: In the production of aerosol medications, the volume of gas propellant used is calculated based on the number of moles needed to deliver the correct dosage.
Practical Applications
- Chemical Analysis: Determining the composition of gases in a mixture by measuring their volumes.
- Environmental Science: Monitoring the concentration of pollutants in the atmosphere by measuring the volume of gas samples.
- Food Industry: Packaging of food products in inert gases to preserve freshness. The volume of gas used is calculated based on the number of moles required to fill the packaging.
Summary
Avogadro’s Law is fundamental in understanding the behavior of gases. It is crucial for various scientific and industrial applications, from breathing and balloon inflation to large-scale chemical manufacturing and environmental monitoring.
Gay-Lussac's Law
Gay-Lussac’s Law
Definition: Gay-Lussac’s Law states that the pressure of a given mass of gas varies directly with the absolute temperature when the volume is kept constant. Mathematically, it is expressed as: \([ P \propto T ]\) or \([ \frac{P}{T} = k ]\) where ( P ) is the pressure, ( T ) is the absolute temperature, and ( k ) is a constant.
Formula: \([ \frac{P_1}{T_1} = \frac{P_2}{T_2} ]\) This equation shows that if the temperature of a gas changes, the pressure changes proportionally, assuming constant volume.
Graphical Representation: A graph of pressure (( P )) versus temperature (( T )) at constant volume is a straight line passing through the origin, indicating direct proportionality.

Real-Life Examples:
- Pressure Cookers: The pressure inside a pressure cooker increases as the temperature increases, cooking food faster.
- Aerosol Cans: When heated, the pressure inside the can increases, which can cause the can to burst if the temperature gets too high.
Industrial Applications:
- Gas Storage: Understanding the relationship between pressure and temperature helps in safely storing gases.
- Automotive Industry: Tire pressure monitoring systems rely on Gay-Lussac’s Law to alert drivers when tire pressure is too low or too high.
Law of Definite Proportions
Law of Definite Proportions
Definition: The Law of Definite Proportions, also known as Proust’s Law, states that a chemical compound always contains exactly the same proportion of elements by mass.
Example: Water \(( \text{H}_2\text{O} )\) always contains hydrogen and oxygen in a mass ratio of 1:8, regardless of the source or method of preparation.
Historical Context: Formulated by Joseph Proust in 1799, this law was fundamental in establishing the concept of chemical compounds having fixed compositions.
Applications:
- Chemical Analysis: Used to determine the purity of a substance.
- Pharmaceuticals: Ensures that drugs have the correct composition for efficacy and safety.
Balancing Chemical Equations
Balancing Chemical Equations
Importance: Balancing chemical equations is essential for understanding the stoichiometry of reactions, ensuring the conservation of mass and atoms.
Steps to Balance Equations:
- Write the Unbalanced Equation: List the reactants and products.
- Count Atoms of Each Element: On both sides of the equation.
- Add Coefficients: Adjust coefficients to balance the number of atoms of each element on both sides.
- Check Your Work: Ensure that the equation is balanced.
Example: Balancing the combustion of methane: \([ \text{CH}_4 + \text{O}_2 \rightarrow \text{CO}_2 + \text{H}_2\text{O} ]\) Balanced Equation: \([ \text{CH}_4 + 2\text{O}_2 \rightarrow \text{CO}_2 + 2\text{H}_2\text{O} ]\)
Applications:
- Chemical Manufacturing: Ensures the correct proportions of reactants are used.
- Environmental Science: Helps in understanding pollutant formation and control.
States of Matter
States of Matter
Definition: Matter exists in three primary states: solid, liquid, and gas. Each state has distinct physical properties.
Properties:
- Solids: Definite shape and volume, strong intermolecular forces.
- Liquids: Definite volume but no definite shape, moderate intermolecular forces.
- Gases: No definite shape or volume, weak intermolecular forces.
Phase Transitions:
- Melting: Solid to liquid.
- Freezing: Liquid to solid.
- Vaporization: Liquid to gas.
- Condensation: Gas to liquid.
- Sublimation: Solid to gas.
- Deposition: Gas to solid.
Applications:
- Material Science: Understanding properties of materials in different states.
- Engineering: Designing systems that involve phase changes, like refrigeration.
Nature of Matter
Nature of Matter
Definition: Matter is anything that has mass and occupies space. It is composed of atoms and molecules.
Dual Nature: Matter exhibits both particle and wave properties, as demonstrated by the wave-particle duality in quantum mechanics.
Key Concepts:
- Atoms and Molecules: Basic building blocks of matter.
- Subatomic Particles: Protons, neutrons, and electrons.
- Quantum Mechanics: Describes the behavior of particles at atomic and subatomic levels.
Applications:
- Nanotechnology: Manipulating matter at the atomic level.
Quantum Computing: Utilizing quantum states of matter for computation.
Classification of Matter
Classification of Matter
Definition: Matter can be classified based on its physical and chemical properties.
Physical Classification:
- Solids: Fixed shape and volume.
- Liquids: Fixed volume, shape of the container.
- Gases: Neither fixed shape nor volume.
Chemical Classification:
- Elements: Pure substances consisting of one type of atom.
- Compounds: Substances formed from two or more elements in fixed ratios.
- Mixtures: Combinations of two or more substances that retain their individual properties.
Applications:
- Chemical Engineering: Designing processes to separate and combine substances.
- Pharmaceuticals: Formulating drugs with precise compositions.

